Problema ‘Il maggiore di una sequenza di numeri’

Problema. Data una sequenza di numeri, trovare il maggiore.

Soluzione proposta. Per determinare il maggiore di una sequenza di numeri si può pensare di procedere nel modo seguente:

• Prelevare il primo numero.
• Procurarsi gli altri numeri uno alla volta e ogni volta memorizzare solo quello che risulta essere il maggiore fino a quel momento.

Adottando questa strategia risolutiva si osserva che dopo la lettura del primo numero e la sua memorizzazione in una variabile (max), si individuano alcune azioni che si ripetono:

1. Lettura di un nuovo numero della sequenza (memorizzazione in una variabile, v).
2. Confronto del numero appena letto con quello che risulta essere il maggiore fra i numeri letti fino a quel momento e che si trova nella variabile max.
3. Quindi, aggiornamento della variabile max se il nuovo numero letto risulta essere maggiore.

I passi individuati vanno ripetuti un numero di volte (che possiamo contare utilizzando una variabile contatore, c) pari a quanti sono i numeri della sequenza (q) meno uno. Il valore di q non è noto a priori e possiamo richiederlo in input.

Con le variabili individuate durante l’analisi e descritte nella seguente tabella, si ottiene il seguente algoritmo.

Flow chart e pseudocodice dell’algoritmo

L’algoritmo precedente può essere riscritto portando all’interno del ciclo anche la lettura del primo numero, nel modo seguente:

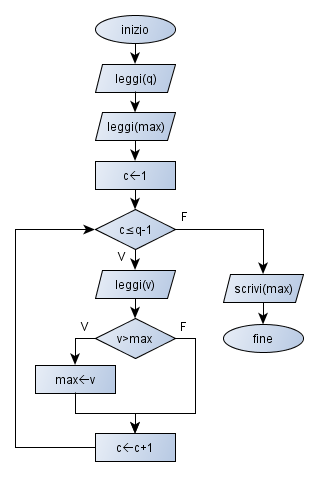
Flow chart e pseudocodice dell’algoritmo equivalente finale

In questo algoritmo la prima iterazione del ciclo fa una cosa diversa rispetto alle iterazioni successive: con la prima iterazione nella variabile max viene memorizzato il primo valore della sequenza; con le iterazioni successive, invece, la variabile max viene aggiornata con il nuovo valore letto, solo se esso risulta maggiore di quello già presente nella variabile max.

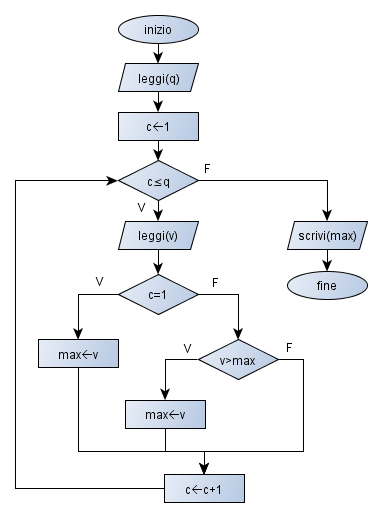
P.S. Il secondo algoritmo progettato facilita l’attività di debugging, in particolar modo per quel che riguarda la gestione degli errori di runtime dovuti agli input non validi (per approfondimenti: La gestione strutturata degli errori di runtime).