Problema ‘Divisibilità fra numeri interi positivi’

Problema. Dati n e k, entrambi numeri interi positivi, stabilire se n è divisibile per k.

Soluzione proposta. Si tratta di valutare la divisibilità fra due numeri interi positivi. La soluzione del problema può basarsi sulla definizione stessa di divisibilità fra due numeri e, quindi, la strategia risolutiva può concentrarsi sul resto della divisione fra i due numeri: se il resto della divisione di n per k è uguale a 0, allora n è divisibile per k.

Come la strategia risolutiva trovata può essere messa in atto, dipende dalle caratteristiche dell’esecutore.

CASO 1.   Nell’ipotesi che l’esecutore sappia calcolare il resto della divisione fra due numeri interi (è questo il caso se si considera l’operatore aritmetico MOD, messo a disposizione da Visual Basic o l’equivalente operatore dei linguaggi “C like” detto modulo o resto, %), la soluzione del problema diventa banale. La strategia risolutiva trovata prima, infatti, in questo caso può essere messa in atto alla lettera: basta calcolare il resto della divisione fra n e k, se il resto è 0, allora potremo dire che n è divisibile per k, altrimenti diremo che n non è divisibile.

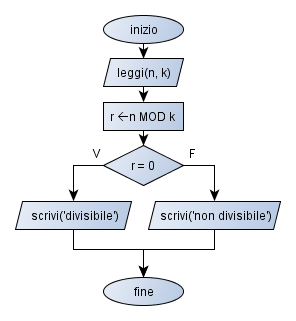
Segue la descrizione dell’algoritmo trovato, sia in pseudolinguaggio, sia in flow-chart.

CASO 2.   Senza l’ipotesi precedente, invece, le cose si complicano un po’ (e può essere didatticamente interessante vedere cosa succede). Ipotizziamo, quindi, che l’esecutore non sappia calcolare il resto della divisione fra due numeri interi. Si noti che il problema da affrontare è identico a quello del caso precedente, ad eccezione del fatto che ora coinvolge anche la soluzione di un sottoproblema, quello di come calcolare il resto della divisione intera. Possiamo ancora proficuamente sfruttare la strategia risolutiva individuata prima, però questa volta non potendo ottenere direttamente il resto della divisione, dobbiamo affrontare anche questo sottoproblema che potremmo risolvere, ad esempio, osservando che: n è divisibile per k se k “entra” in n esattamente un numero intero di volte.

Ciò può essere verificato sottraendo ripetutamente k ad n (con l’istruzione: n=n-k) fintanto che questa differenza si mantiene maggiore o uguale a k (la condizione di controllo del ciclo pre-condizionale col mentre è: n≥k). Quando la differenza diventa minore di k o uguale a 0, allora essa ci darà proprio il resto della divisione.

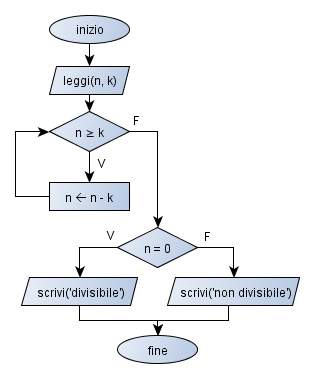
Segue la descrizione dell’algoritmo trovato, sia in pseudolinguaggio, sia in flow-chart.